Rezervuar Problemi
Sifon haznesi, sabit debi ile dolarken belirli bir seviyeden
sonra, doluluğuna bağlı olarak debisi azalmaktadır. Haznedeki su yüksekliği ile
zaman arasında bağlantı kurulabilir mi? Kurulabilirse bu bağlantı nedir?
Q su debisi, y haznedeki su yüksekliği ve q0 azami
ya da başlangıç debisi olmak üzere:
Şeklinde modellenebilir. Burada u, debinin azalmaya başladığı
yüksekliktir. Bu yüksekliğin üzerinde Q y’nin bir fonksiyonu ile azalır. Çünkü
her y için tek bir y-u değeri vardır ve her bir y-u değeri için debi sadece tek
bir değer alır. Yani:
O halde:
Şeklinde sürekli bir f fonksiyonu tanımlanabilir. Çok basit bir
model olması açısından,
Şeklinde tanımlansın. Yani u’yu geçen her mesafenin bir k katı
kadar debide azalma meydana gelsin. Şimdi de debinin tanımından faydalanarak
y(t) ifadesi yapabileceğimiz diferansiyel denklemi elde edelim:
Böylece iki parça için elde edilen denklemler:
Birinci mertebeden ayrıştırılabilir ve lineer diferansiyel
denklemleri bulunur. [I] no’lu denklem için başlangıç
koşulu t=0 için y=0’dır. Ve çözümü uzatmadan şu şekildedir:
Parçanın aralığını belirleyecek olursak, yani u=y(t0)
sağlayan t0 değeri:
Q0 başlangıç debisinin A’ya bölümünü, v0
ile gösterip kendisine y’nin başlangıçtaki değişim oranı veya y’nin azami
değişim oranı diyelim. Zaten debi artmayacağından bu problem için ikisi aynı
şeydir.
[II] no’lu denklem için sınır değeri
t=t0 için y=u’dur. Ve bu şekilde y(t) parçalı fonksiyonu sürekli
olacak şekildedir. [II] no’lu denklem birinci
mertebeden lineer diferansiyel denklemdir ve genel çözümü:
Olup, k/A = τ ile gösterecek
olursak:
Başlangıç koşulu ile C sayısı bulunabilir. Böylece:
Bulunup ikinci parça için Y(t):
Elde edilir. O halde genel ifadesi ile Y:
Sabitlere değerler verip fonksiyonu çizdirmeden önce, y’nin
sürekli ve sonsuzda bir değere yakınsadığını gözlemleyebiliriz. (Fonksiyon
sürekli olduğu gibi türevi de süreklidir.)
Bir dolma süresi belirleyecek olursak, bu tarz bir fonksiyon
için sonsuz çıkar. Su yüksekliğini bir tolerans değerinden daha hassas yer
değiştirmediği düşünülerek; debinin değişim oranının tolerans değeri altına indiği
tau’yu belirleyebiliriz. TD bu belirlenen tolerans
değeri olmak üzere:
K burada kesilmesi için verilen toleransa göre belirlenecek olan
bir sabittir. Şimdi değerler vererek eğriyi çizdirelim. Gerçeğe yakın ölçülerle
çalışacak olursak: taban alanı 0.2 m^2; kısılmaya başladığı yükseklik (u) 0.5 m;
başlangıç hızı (v_0) 0.025 m/s; yaklaşık 15 cm sonra debinin tamamen durduğunu
düşünürsek de,
Toleransı 1 mm/s olarak belirlersek, K yaklaşık olarak -3 çıkar.
Dolum süresi de
Bulunur.
F fonksiyonu, yani y ile debi arasındaki ilişki, çok basit
modellenmişti. Nonlineer modellenirse diferansiyel denklemin çözümü
zorlaşabilir. Çözüm bulunsa bile y(t) şeklinde yazılamayabilir. F fonksiyonu
sayısal olarak [yi Qi] ikilileri ile deneysel olarak da
modellenebilir. Yine interpolasyon eğrileri
uydurularak çözülebilir. Ancak tüm bunların yanında sayısal olarak da
çözülebilir.
Yukarıdaki işlemlerde kesit alanının sabit olduğu düşünülmüştü.
Gibi hesaba katılırsa ve y’ye bağlı bir fonksiyonla ifade
edilecek olursa:
Haline gelir. Ve böylece
Diferansiyel denklemi bulunur. Aynı başlangıç koşulu ile
çözülerek t ile Y ilişkilendirilebilir.


















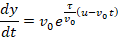








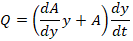



Hiç yorum yok:
Yorum Gönder