Problemin tam tanımını bir örnek ile canlandırmaya çalışalım.
Bir tahterevalli düşünelim. Her iki oturma yerinde de birer çocuğun oturduğu
bir tahterevalli olsun. Dengede olma koşulu, döner mafsal eksenine olan momentlerin
sıfır olmasıyla sağlanır. Her çocuğun oturduğu yerden ağırlığı şiddetince
moment değeri vardır. Fakat tam olarak kuvvetin etki ettiği nokta neresidir?
Örneğin bir tarafta 2 çocuk bulunsun. Veya 4, 8, 10 hatta sonsuz tane. Yayılı
bir yük şeklinde etki ettiğinde tam olarak etki noktası neresi olur? Veya
çocuklardan birinin poposu öylesine geniş olsun ki çocuğun oluşturacağı
kuvvetin kuvvet kolunu seçmek zorlaşsın. Bu yazıda, kütle merkezi veya kuvvet
merkezi gibi tanımlar yardımıyla bu problemin daha sistematik ve daha kolay
çözülebildiğini göstermeyi amaçlıyorum. Öte yandan bu süreç öylesine sezgisel
ki kimse bununla ilgili bir ispat beklemiyor da olabilir. Ancak bu sayede kütle
merkezi tanımının aslında ne kadar manidar olduğunu anlaşılmış olacaktır.
Tek boyutlu bir yayılı yük düşünelim. Yayılı yük ile meydana
gelen toplam kuvveti kolayca hesap edebiliriz.
Ve bildiğimiz gibi kuvvet merkezi, o nokta etrafında herhangi
bir toplam momentin oluşmadığı nokta olarak canlandırılabilir. Nitekim yayılı
kuvvetin orijine göre olan tüm momentlerinin ifadesi şu şekildedir:
Aynı moment bu merkeze toplam kuvvet cinsinden ifade
edilebilir ki bu kuvvet merkezinin yeridir. Kuvvet merkezini 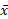 ile gösterelim ve merkez şu şekilde bulunur:
ile gösterelim ve merkez şu şekilde bulunur:
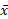 ile gösterelim ve merkez şu şekilde bulunur:
ile gösterelim ve merkez şu şekilde bulunur:
Yukarıdaki eşitlik aynı zamanda şudur:
Kuvvet merkezine göre momentler toplamının sıfıra eşit olduğunu
gösterelim:
Dolayısıyla bu nokta öyle bir noktadır ki eğer yayılı yükü o
noktadan döner mafsal ile bağlasak (veya o noktadan bir parça ile dengelesek)
parça herhangi bir tarafa düşmez: denge noktasıdır.
Yayılı bir yükün, yükün tanımlı olduğu küme içerisinde veya
dışarısında olan herhangi bir noktaya göre momentini aldığımızda, her bir
noktaya dağılmış olan yükün oluşturduğu tüm momentleri toplamamız gerekir. 2
tane çocuğun olduğu tahterevalli örneğini hatırlayalım. Sırayla her iki çocuğun
momentleri toplanır. Yayılı yük, belirli bir mesafeye sonsuz çocuğun
sığdırılması benzetilebilir. Tüm çocukların teker teker momentlerinin alınması
gerekir.
Örneğin bir A kümesi içerisinde tanımlanan yayılı yükü ele
alalım. Tüm yüklerin P noktasına göre momentini alalım.
Bu hesabın neticesinde yükün oluşturduğu moment bulunur. Fakat
bu integralin alınması yerine bazı alternatifler uygulanabilir.
Kuvvet merkezi tanımını kullanarak bu hesabı integral dışında
hesap edebiliriz.
Dolayısıyla görülüyor ki yayılı yükün kuvvet merkezinden olan
mesafe doğrudan moment koludur. Bu yöntemle yayılı yük tipi ile moment hesabı
farklı iki kategoride analiz edilebilir.
Daha genel bir ifade ile bu durum daha fazla boyutlu
durumlardaki normal yüklemeler için de geçerlidir. Kuvvetlerin sadece yüzeye
dik olduklarını düşünmek (örneğin tavadaki bir salamın ağırlığı ile oluşturduğu
bası gibi) tanımlamaları daha da kolaylaştıracaktır.
Benzer şekilde tüm momentlerin ifadesi de yazılabilir.
Benzer şekilde yüklemenin, P noktasına olan kuvvet kolu vektörü
yerine, A kümesi içerindeki kuvvet merkezi noktasına göre olan vektör cinsinden
eşiti yazılabilir. Burada, kuvvet merkezi noktası  ve bu noktaya göre olan konumlar ise
ve bu noktaya göre olan konumlar ise  ile
gösterilsin.
ile
gösterilsin.
 ve bu noktaya göre olan konumlar ise
ve bu noktaya göre olan konumlar ise  ile
gösterilsin.
ile
gösterilsin.
Dikkat edilirse buradaki terimlerden biri, yüklemenin kendi
içindeki momentleridir. Dolayısıyla son terimin değeri sıfıra eşittir. Kuvvet
merkezi ise tanımı kullanılarak bu gösterilebilir.
Sonuç olarak toplam moment, yayılı yükün merkezinden olan
mesafenin kuvvet kolu olarak kullanılabileceğidir.













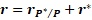





Hiç yorum yok:
Yorum Gönder