1. Lülede Akış
Lüleler, bir kanal
boyunca akışkanın kinetik enerjisi ile basıncı arasında değişimini
gerçekleştirir. Lüle boyunca akış için bazı varsayımlar yapılabilir:
·
Akış boyunca ısı alışverişi
yoktur.
·
Akış boyunca hal değişimi
tersinirdir.
·
Akış boyunca oluşacak sürtünme
etkileri azdır. (Umur, 2009)
Dolayısıyla akışın
izantropik olduğu varsayılacaktır.
1.1. Sıkıştırılamaz Akış
Şekil 1 Daralan lüle (Covergent
nozzle)
(Şekil 1)’de daralan bir lüle bulunmaktadır. Sıkıştırılamaz bir akış için
süreklilik denklemi, giriş ve çıkış arasındaki enerji denklemi (Bernoulli
Prensibi) yazılabilir.
1
|
|
2
|
Böylece (1) ve (2) bağıntıları kullanılarak, giriş parametrelerinin ve sınır
parametrelerinden birinin bilinmesi ile tüm özellikler bulunabilir.
1.2. Sıkıştırılabilir Akış
Sıkıştırılamaz akışta
açıktır ki, kesit alanının daraltılması ile akışkanın basıncı kinetik enerjiye
dönüştürülebilir. Ancak akışkanın basınç altında yoğunluğu değiştiği dikkate
alınırsa, yoğunluğu veren bağıntı:
3
|
Enerji korunumunu veren
bağıntı, (h: entalpi):
4
|
Ve tersinir adyabatik hal
değişimini veren durum denklemi:
5
|
Ve
süreklilik denklemi kullanılarak akış boyunca tüm parametreler benzer şekilde
elde edilebilir. Entalpi miktarına kinetik enerjinin eklenmesi ile elde edilen
enerjiye durgunluk (veya toplam) entalpi adı verilir. (Çengel & Cimbala,
2006)
6
|
2. Mach Sayısının Etkisi
Süreklilik denklemi,
logaritmik diferansiyel form:
7
|
Yapılmış kabuller
altındaki enerji ifadesinin diferansiyel formu:
8
|
İzantropik hal değişimi
durumundaki diferansiyel ilişki:
9
|
Lülenin alanı ile hız
arasındaki ilişki inceleceğinden dolayı, (7)
denklemindeki yoğunluk, hız cinsinden ifade edilecektir. (8) ve (9) denklemlerinde entalpi yok edilirse ve ideal gaz bağıntısı kullanılırsa:
10
|
Böylece yoğunluk, ideal
gaz yasasının diferansiyel ifadesi kullanılarak:
11
|
(9) ve (10) , (11)’de yerine yazılırsa,
12
|
Şimdi, süreklilik
denkleminde (12) yerine yazılırsa:
13
|
Burada c, ses hızı
olmak üzere,
O halde (13) ifadesi:
14
|
3. Hızlanan ve Yavaşlayan Akış
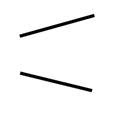
Kesit alanındaki
değişim ile hızdaki değişim incelenecek olursa,
o Kesit daraldıkça (dA<0) hız artar (dU>0): Hızlanan akış
o Kesit genişledikçe
(dA>0) hız azalır
(dU<0): Yavaşlayan akış
o Kesit daraldıkça (dA<0) hız azalır
(dU<0): Yavaşlayan akış
o Kesit genişledikçe (dA>0) hız artar (dU>0): Hızlanan akış
Tablo 1 Mach sayısına göre hızlanan ve yavaşlayan akış
4. Durgunluk Değerleri
Durgunluk entalpisi
yazılacak olursa,
15
|
16
|
Böylece,
17
|
Elde edilir. Böylece
aşağıdaki durgunluk bağıntıları elde edilir (Çengel & Cimbala, 2006):
5. Lülede Akış Örneği
Çözüm:
O halde,
Kesitler oranını süreklilik
denklemi ile elde edebiliriz. Öncelikle ideal gaz yasasını kullanarak
yoğunlukları elde edelim.
Tablo 2 Basınç düşümlerine karşılık akışkan özellikleri
Mach sayısına karşılık
hesaplanan alan değerleri grafik halinde verilirse,
Şekil 2 Mach sayısına karşılık kesit alanı değerleri
6. Başvurular
Çengel,
Y., & Cimbala, J. (2006). Fluid
Mechanics Fundamentals And Applications.
Mattingly, J. D. (2005). Elements of Propulsion: Gas Turbines and Rockets. New Delhi:
McGraw-Hill Education.
Umur, H. (2009). Akışkanlar
Mekaniği (4 b.). Dora Yayın Dağıtım.



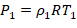













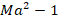












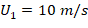































Hiç yorum yok:
Yorum Gönder